Vamos fazer um pequeno resumo dos conjuntos númericos, suas relações e possíveis aplicações.
Números Naturais
O conjunto dos números naturais tem como representação a letra maiúscula N e estes são compostos pelos algarismos : 0, 1, 2, 3, 4, 5, 6, 7,
8, 9, que também são conhecidos como algarismos indo-arábicos.
Um pouco de História do conjunto dos números Naturais.
A origem dos números naturais advém dos processo de troca, a buscar de novas necessidade de sobrevivência trouxe ao homem antigo a possibilidade de adquirir , controlar seus bens e alimentos este processo criou a necessidade de contar , estabelecer critérios de contagem . Veja mais sobre a história....
.http://pessoal.sercomtel.com.br/matematica/fundam/numeros/numeros.htm
Vejamos a representação dos Números Naturais:
Na sequência consideraremos que os naturais têm início com o número zero e escreveremos este conjunto como:
N = { 0, 1, 2, 3, 4, 5, 6, ...}
Representaremos o conjunto dos números naturais com a letra N. As
reticências (três pontos) indicam que este conjunto não tem fim. N é um
conjunto com infinitos números.
Excluindo o zero do conjunto dos números naturais, o conjunto será representado por:
N* = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...}
Números Inteiros
O conjunto Z dos Números Inteiros
Definimos o conjunto dos números inteiros como a reunião do conjunto
dos números naturais, o conjunto dos opostos dos números naturais e o
zero. Este conjunto é denotado pela letra Z (Zahlen=número em alemão).
Este conjunto pode ser escrito por:
Z = {..., -4, -3, -2, -1, 0, 1, 2, 3, 4,...}
Exemplos de subconjuntos do conjunto Z
(a) Conjunto dos números inteiros excluído o número zero:
Z* = {..., -4, -3, -2, -1, 1, 2, 3, 4,...}
(b) Conjunto dos números inteiros não negativos:
Z+ = {0, 1, 2, 3, 4,...}
(c) Conjunto dos números inteiros não positivos:
Z- = {..., -4, -3, -2, -1, 0}
Observação: Não existe padronização para estas notações.
Reta Numerada
Uma forma de representar geometricamente o conjunto Z é construir uma
reta numerada, considerar o número 0 como a origem e o número 1 em
algum lugar, tomar a unidade de medida como a distância entre 0 e 1 e
por os números inteiros da seguinte maneira:
Números Racionais
O
conjunto dos números racionais é uma ampliação do conjunto dos números
inteiros.
O conjunto formado pelos números racionais positivos,
os números racionais negativos e o zero
são um novo conjunto que chamamos de conjunto dos números racionais e
é representado por Q.
Exemplos:
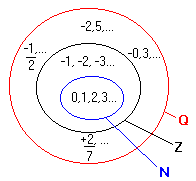
Observe o desenho abaixo:
O conjunto de Q é uma ampliação do conjunto Z.
Outros subconjuntos de Q:
-
Q*
é o conjunto dos números racionais diferentes de zero;
-
Q+
é o conjunto dos números racionais positivos e o zero;
-
Q-
é o conjunto dos números racionais, negativos e o zero;
-
Q+*
é o conjunto dos números racionais e positivos;
-
Q-*
é o conjunto dos números racionais negativos.

fonte:http://www.somatematica.com.br/fundam/racionais2.php
Números Irracionais
Os
números irracionais são aqueles que não podem ser representados por
meio de uma fração. O surgimento desses números veio de um antigo
problema que Pitágoras se recusava a aceitar, que era o cálculo da
diagonal de um quadrado, cujo lado mede 1 unidade, diagonal esta que
mede √2. Este número deu início ao estudo de um novo conjunto,
representado pelos números irracionais.
Veremos alguns exemplos de números
irracionais e notaremos que a sua parte decimal não possui nenhuma
estrutura que possa ser fundamentada em forma de fração, assim como
ocorre em frações periódicas.
Constantes irracionais ou números transcendentais:

Números irracionais obtidos pela raiz quadrada de um número:

Estes são os números irracionais, cujo valor da última casa decimal nunca saberemos.
Números Irracionais (I): √2, √3, –√5, 1,32365498...., 3,141592..
Números Reais
O conjunto dos números reais surge para designar a união
do conjunto dos números racionais e o conjunto dos números irracionais. É
importante lembrar que o conjunto dos números racionais é formado pelos
seguintes conjuntos: Números Naturais e Números Inteiros. Vamos
exemplificar os conjuntos que unidos formam os números reais. Veja:
Números Naturais (N): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, ....
Números Inteiros (Z): ..., –8, –7, –6, –5, –4, –3, – 2, –1, 0, 1, 2, 3, 4, 5, 6, 7, 8, .....
Números Racionais (Q): 1/2, 3/4, 0,25, –5/4,
Números Irracionais (I): √2, √3, –√5, 1,32365498...., 3,141592....
Podemos concluir que o conjunto dos números reais é a união dos seguintes conjuntos:O conjunto dos números reais surge para designar a união
do conjunto dos números racionais e o conjunto dos números irracionais. É
importante lembrar que o conjunto dos números racionais é formado pelos
seguintes conjuntos: Números Naturais e Números Inteiros. Vamos
exemplificar os conjuntos que unidos formam os números reais. Veja:
Números Naturais (N): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, ....
Números Inteiros (Z): ..., –8, –7, –6, –5, –4, –3, – 2, –1, 0, 1, 2, 3, 4, 5, 6, 7, 8, .....
Números Racionais (Q): 1/2, 3/4, 0,25, –5/4,
Números Irracionais (I): √2, √3, –√5, 1,32365498...., 3,141592....
Podemos concluir que o conjunto dos números reais é a união dos seguintes conjuntos:
N U Z U Q U I = R ou Q U I = R

N U Z U Q U I = R ou Q U I = R
Vejamos alguns vídeos que aplicam os conceitos acima tratados e outros para aprofundamentos.
Matemática - Aula 1 - Conjuntos
http://www.youtube.com/watch?v=1zxL3MYdK04 (Primeira Parte)
http://www.youtube.com/watch?v=bQ42UcLEjoY (Segunda Parte)
http://www.youtube.com/watch?v=XetNn3fNjMo (Terceira Parte)
http://www.youtube.com/watch?v=ERrIYN-TIIo (Quarta Parte)
http://www.youtube.com/watch?v=FWs4qBxo_dw (Quinta Parte)
http://www.youtube.com/watch?v=Fdw3EMxVGv4 (Sexta Parte - Final)
Matemática - Aula 2 - Conjuntos Numéricos
http://www.youtube.com/watch?v=FL6WQG6Z5tQ (Primeira Parte)
http://www.youtube.com/watch?v=19Gx6x5EKIg (Segunda Parte)
http://www.youtube.com/watch?v=5luhLfmp6ig (Terceira Parte - Final)
Referência
mauriciomunhoz.blogspot.com
aaa