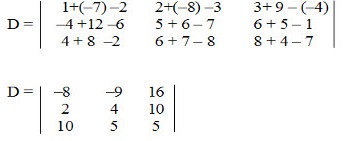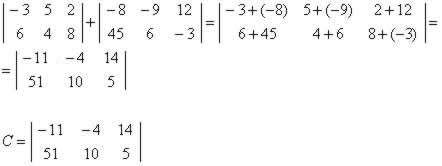Matrizes - parte 1

O entendimento da  conceituação de matriz, precisamos aderir à convenção dos matemáticos em que a ordenação das linhas de uma matriz seja dada de cima para baixo, e a ordenação das colunas, da esquerda para a direita.

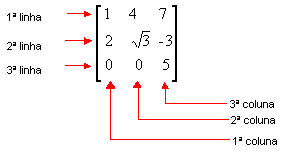
No visão mais ampla: uma matriz m x n, com m e n números naturais não nulos, é toda tabela composta por m.n elementos dispostos em m linhas e n colunas.
A representação de uma matriz é, em geral, será por uma letra maiúscula do nosso alfabeto (A, B, C, ...Z), enquanto os seus termos são representados pela mesma letra, desta vez minúscula, acompanhada de dois índices (a₁₁   a₁₂   a_{13 ...} a_mn), onde o primeiro representa a linha e o segundo a coluna em que o elemento está localizado.


Vamos Assistir um vídeo explicativo.
1º vídeo



2º Vídeo


Exercícios

1)Dadas as matrizes  ,    e   , determine a matriz D resultante da operação A + B – C.

2)Determine a matriz C, resultado da soma das matrizes A e B.

3)Considerando as matrizes:

Determine:

a) A + B – C
b) A – B – C

Correção exercícios 1, 2 e 3

Resposta Questão 1

• Resposta Questão 2
  
  
Resposta Questão 3

• 
  

Equação do 2º grau

Equação do 1º grau - parte 1
O que é uma equação do 2º grau?

Ele segue o princípio da equação do 1º grau, que é uma igualdade, a diferença que o expoente mais da incógnita nesta equação é o número 2, o seja do 2º grau.


Vamos para parte prática de tentar resolver uma equação, acompanhe o vídeo com a explicação.


Vamos ao seu desafio, após assistir ao vídeo resolva as equações.

Resolvendo equações

a)x² – 10 x + 9 = 0

resposta

x^’= 9 e x^’’ = 1

b) x²+ 2x – 8 = 0

resposta

x’=-4   e x”= 2

c) x²- 6x + 9 = 0

x’= 3  e x’’=3

Referências

mauriciomunhoz.blogspot.com.br

Equações do 1º grau

Equação do 1º grau

O que é uma equação do 1º grau?
]
Vamos separar em etapas, a equação é representada por um sinal matemático. Qual?
 - O sinal da igualdade
 
Mais também tem a representação de incógnita a mais utilizada é a letra x.  
No desenho em amarelo temos bem um representação da igualdade que é a balança, no caso verifica-se que letras na balança.
O objetivo da balança é igual, o seja o que tem de um lado também terá que ter do outro.
Mais vamos aqui trabalhar com método básico de equação do 1º grau.Convido você para resolver 3 exercícios de cada exemplo apresentado. Vamos lá:
1º vídeo:


Exercícios:

Resolva as equações abaixo:
a) 3x= -9 
b)-2x= 24
c)  3x= -7

Respostas:
a) -3
b) -12
c) -7/3

2º vídeo



Exercícios
a) 3x + 3 = 30
b) 2x - 10 = 40
c) -5x + 5 = 50

Respostas:
a) 9
b) 25
c) - 9

3º Vídeo



Exercícios
a) 2x + 4 = x + 5
b) 5x - 2 = 10 + 2x
c) -3x + 4 =  x + 12

Respostas:

a) 1
b) 4
c) -2

4º Vídeo



Exercícios
a) 2(x+ 6) = 20
b) 5( x - 4) = - 50
c) 4( x - 1) =  - 2 ( x - 1)

Respostas

a) 4
b) -6
c) 1

5º Vídeo



Exercícios

a) x +  2 = 6
    2
b) x + 5 = 20
    3
c) 2x + 4 = 5 + x
    3

Respostas
a) 8
b) 45
c) 9/2

6º Vídeo



Exercícios

a) x+ 3 + 2 = 25
      2

b) 2x + 5 = 5 + x-1
         3              5

c) x + 5  + 1 = 6
       2

Respostas:

a) 23
b) 47/7
c) 5

7º Vídeo



Exercícios

a)  x =  7
     4     2

b)  3 =  2
     x     8
c)  3 =  5
     6     x

Respostas
a) 14
b) 12
c) 10


Referência
mauriciomunhoz.blogspot.com.br