Primeiramente vamos estudar os conceitos fundamentais da geometria, que são :
- Ponto
- Reta
- Plano
O ponto, a reta e o plano.
Primeiro vamos saber quem foi Euclide.
Primeiro vamos saber quem foi Euclide.
Euclides era um matemático grego, viveu em Alexandria na primeira metade
do séc. III a.C. Acredita-se que ele era mais novo que os primeiros
discípulos de Platão e mais velho que os de Arquimedes. É muito provável
que Euclides tenha recebido ensinamentos matemáticos dos primeiros
discípulos de Platão.

Euclides estudou os elementos primitivos (ponto, reta e plano) e formulou a Geometria Euclidiana.
Representamos o ponto por qualquer letra maiúscula do alfabeto, a reta por qualquer letra minúscula e o plano por letras gregas (α: alfa, β: beta e γ: gama). Acesse um pouco mais da bibliográfia de Euclides.
Ponto: É a mais simples representação que encontramos, um toque com o lápis no papel já se constrói um ponto, o ponto pode ser algo localizado no espaço, como um furo, uma estrela no céu, o centro do campo de futebol, etc.
Representamos o ponto por qualquer letra maiúscula do alfabeto, a reta por qualquer letra minúscula e o plano por letras gregas (α: alfa, β: beta e γ: gama). Acesse um pouco mais da bibliográfia de Euclides.
Ponto: É a mais simples representação que encontramos, um toque com o lápis no papel já se constrói um ponto, o ponto pode ser algo localizado no espaço, como um furo, uma estrela no céu, o centro do campo de futebol, etc.

Reta:A dedução lógica de uma reta é um linha traçada numa única direção, podemos dizer que a reta é formada por infinitos pontos, como uma régua,, uma corda esticada,uma rua plana, lados de um campo de futebol, as traves do gol, os raios solares, etc.

Plano: O conceito de plano é algo mais complexo, temos a noção de plano pela superfície de uma parede, o chão, um quadro, universo, etc.

Posições de retas no plano
Paralelas: retas que não possuem nenhum ponto em comum.

Concorrentes: retas que possuem um ponto em comum.

Perpendiculares: retas que possuem um ponto em comum e formam um ângulo de 90º.

Semirreta: possui origem em um ponto, tornando-se infinita no sentido contrário.

Segmento de reta: possui origem e fim.
O que são ângulo?
Um pouco de história....
O conceito de ângulo aparece primeiramente em materiais gregos no estudo
de relações envolvendo elementos de um círculo junto com o estudo de arcos
e cordas. As propriedades das cordas, como medidas de ângulos centrais ou
inscritas em círculos, eram conhecidas desde o tempo de Hipócrates e talvez
Eudoxo tenha usado razões e medidas de ângulos na determinação das dimensões
do planeta Terra e no cálculo de distâncias relativas entre o Sol e a Terra.
Eratóstenes de Cirene (276 a.C.-194 a.C) já tratava de problemas relacionados
com métodos sistemáticos de uso de ângulos e cordas.
Desde os tempos mais antigos, os povos vêm olhando para o céu na tentativa
de encontrar respostas para a vida tanto na Terra assim como entender os corpos
celestes que aparecem à nossa vista. Assim, a Astronomia talvez tenha sido
a primeira ciência a incorporar o estudo de ângulos como uma aplicação da
Matemática.
Na determinação de um calendário ou de uma hora do dia, havia a necessidade
de realizar contagens e medidas de distâncias. Frequentemente, o Sol servia
como referência e a determinação da hora dependia da inclinação do Sol e da
relativa sombra projetada sobre um certo indicador (relógio de Sol).
Para obter a distância que a Lua estava acima do horizonte, dever-se-ia calcular
uma distância que nunca poderia ser medida por um ser humano comum. Para resolver
este problema, esticava-se o braço e se calculava quantos dedos comportava
o espaço entre a Lua e o horizonte ou então, segurava-se um fio entre as mãos
afastadas do corpo e se media a distância.
Os braços deveriam permanecer bem esticados para que a resposta fosse a mais
fiel possível. A medida era diferente de uma medida comum e este modo foi
o primeiro passo para medir um ângulo, objeto este que se tornou importantísimo
no contexto científico.
Na verdade, não se sabe quando o homem começou a medir ângulos, mas se sabe
que estes eram medidos na Mesopotâmia e eram muito bem conhecidos quando Stonehenge
foi construída, 2000 a.C.
O conceito de ângulo
Ângulo é a reunião de dois segmentos de reta orientados (ou duas semi-retas orientadas) a partir de um ponto comum.

A interseção entre os dois segmentos (ou semi-retas) é denominada
vértice do ângulo e os lados do ângulo são os dois segmentos (ou
semi-retas).
Tipos
Classificação de ângulos
Os ângulos são classificados de acordo com suas medidas:
Agudo: ângulo com medida menor que 90º.
Reto: ângulo com medida igual a 90º.
Obtuso: ângulo com medida maior que 90º.
Raso: ângulo com medida igual a 0º ou 180º.
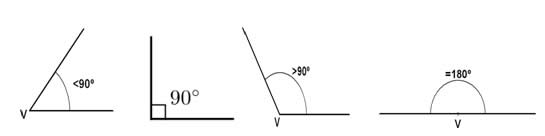
agudo reto obtuso raso
Os ângulos são classificados de acordo com suas medidas:
Agudo: ângulo com medida menor que 90º.
Reto: ângulo com medida igual a 90º.
Obtuso: ângulo com medida maior que 90º.
Raso: ângulo com medida igual a 0º ou 180º.

agudo reto obtuso raso
Atividades:
1)Jogo Educativo:
| Rampa | ||||
| Faça o carro pular sobre os obstáculos, para isso faça os cálculos corretos de velocidade e ângulo. |
2) Medindo os ângulos com o Geogebra:
Fonte:http://odin.mat.ufrgs.br/usuarios/bruno/angulos_transf1/ang_medida1.html
Referências:
www.mauriciomunhoz.blogspot.com
http://pessoal.sercomtel.com.br/matematica/fundam/geometria/geo-ang.htm
http://www.brasilescola.com/matematica/os-primeiros-conceitos.htm
http://www.grupoescolar.com/pesquisa/euclides--matematico.html
http://www.brasilescola.com/matematica/angulos.htm
Nenhum comentário:
Postar um comentário